5. Relacions de grau major que dos

 

Anem a estudiar una miqueta més el cas de les relacions ternàries. Donada la seua complexitat podríem, i de fet així es fa de vegades, descompondre-la en tres relacions binàries

 

 

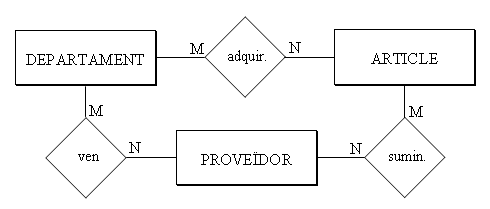
Així pot haver una ocurrència que Comptabilitat adquireix una calculadora, una altra que Comptabilitat compra a Distribucions Garcia, S.L., i una altra que Distribucions Garcia, S.L. subministra calculadores.

Però això no té per què voler dir que la calculadora comprada per Comptabilitat, l'haja comprada a Distribucions Garcia, S.L. Pot haver-la comprada a un altre proveïdor, i el que li compra a Garcia són bolígrafs (encara que Garcia també en puga vendre de calculadores).

En canvi en una relació ternària es diu qui compra, què compra i a qui compra. Per tant una relació ternària proporciona més informació que 3 binàries.

 

 

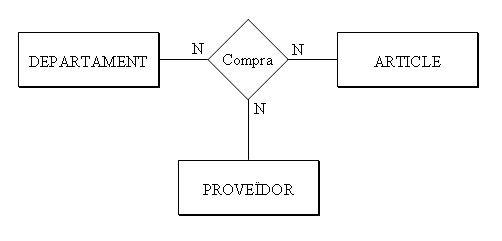
La cardinalitat es calcula fixant-ne 2 i veient quantes ocurrències entren en la tercera. Així, un determinat departament pot comprar un determinat article a més d'un proveïdor (N). Un article d'un proveïdor el pot comprar més d'un departament (N). I un departament pot comprar a un proveïdor més d'un article. No té perquè ser sempre N:N:N (en aquest cas de les ternàries no utilitzarem ja la M, només la N). Per exemple suposem que un departament sempre compra un article al mateix proveïdor; aleshores en Proveïdor tindríem 1.

 

 

 

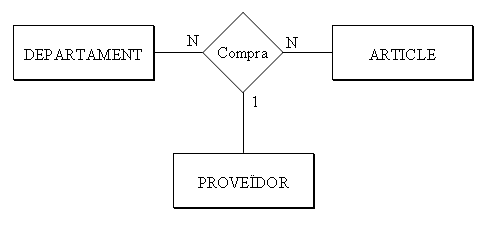
Algunes ferramentes de disseny de B.D. només permeten relacions binàries. Aleshores s'hauria de fer un truc per a representar la relació ternària, construint una entitat nova, dèbil, que depenga en identificació de les altres 3. Veurem les entitats dèbils en el següent punt.